Slope Periodicity Management

The Fourier Transfrom Reconstructor assumes a fully periodic square grid for the phase. Most telescopes are not square, and atmospheric turbulence is not periodic, so we have to use a strategy to account for the non-periodicity in the slope grid. We do this by adding pseudo-slopes outside the telescope aperture, which serve to make the slope domain appear periodic, despite the non-periodic nature of the observed slopes.

Reconstruction on a periodic domain

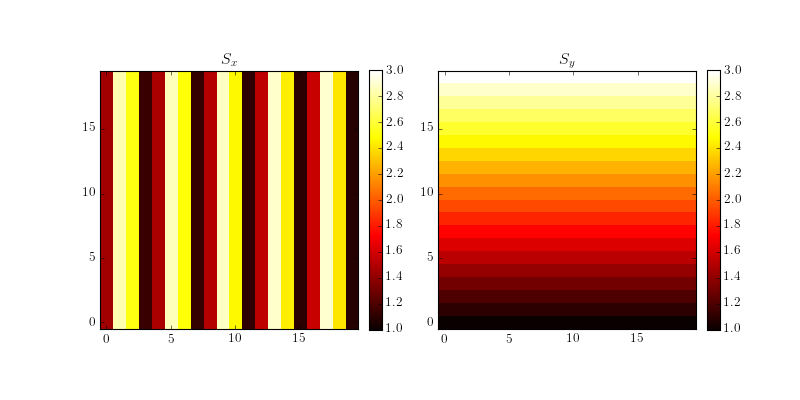
Lets provide some example slopes on a fully periodic domain to work with.:

>>> import numpy as np
>>> sx = -np.sin(np.linspace(-10,20,20)[None,:]) * np.ones((20,1)) + 2
>>> sy = (np.linspace(-1,1,20)[:,None]) * np.ones((1,20)) + 2

These slopes are both periodic on the full fourier grid, and can be reconstructed with a pure Fourier Transform Reconstructor.

(Source code, png, hires.png, pdf)

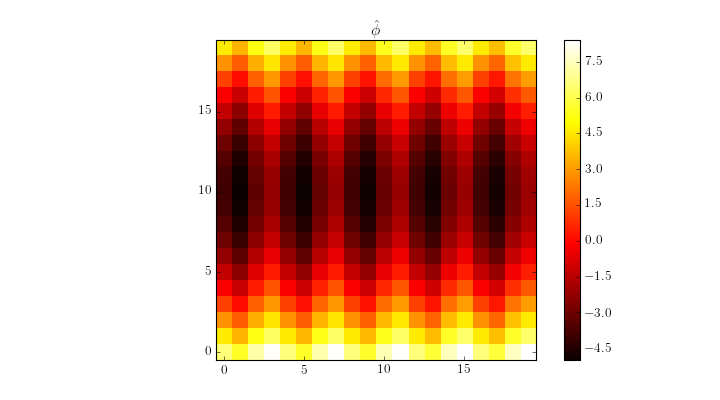
Reconstructing these slopes with the Fourier Transform Reconstructor is quite easy:

>>> from FTR import FourierTransformReconstructor as FTRecon
>>> recon = FTRecon(np.ones((20,20)), filter='mod_hud', suppress_tt=True)
>>> phi = recon(sx, sy)

(Source code, png, hires.png, pdf)

Reconstruction without slope management

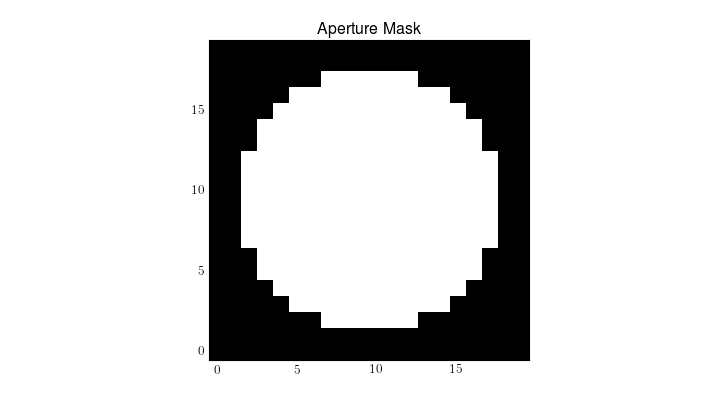
First, let’s set up a circular aperture for our telescope. We’ll skip any central obscuration, though in general this shouldn’t provide a problem, as the secondary obscuration is continuous across the subapertures.:

>>> from FTR.utils import circle_aperture
>>> ap = circle_aperture((20, 20), 8)

(Source code, png, hires.png, pdf)

We can naievely use the pure Fourier Transform Reconstructor on apertured slopes:

>>> recon = FTRecon(ap, filter='mod_hud', suppress_tt=True)
>>> phi_ap = recon(sx * ap, sy * ap)

(Source code, png, hires.png, pdf)

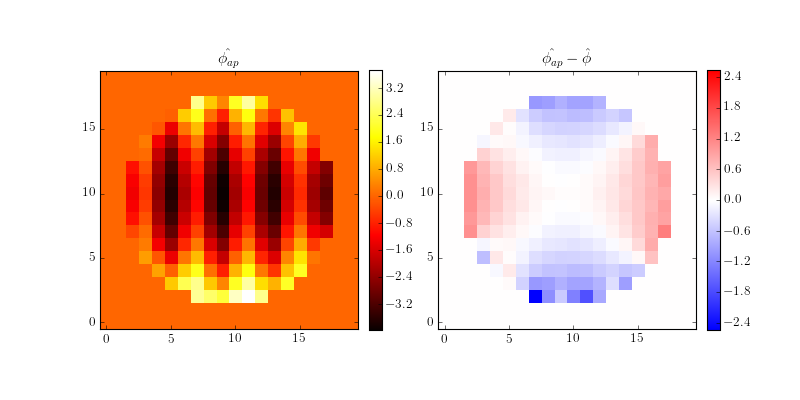
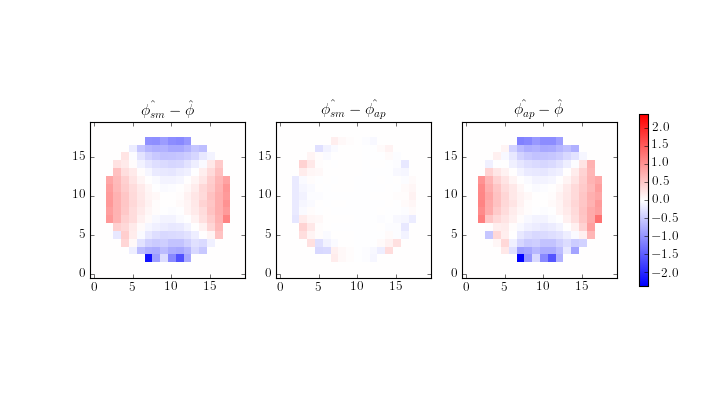
This leaves a characteristic residual pattern around the edge of the aperture.

Reconstruction with slope management

To improve the reconstruction with an aperture, we apply additional slopes outside the aperture which correct for the periodicity of the system.

Using a the slope-managed reconstructor, we get a much better reconstruction:

>>> from FTR.slopemanage import SlopeManagedFTR
>>> recon = SlopeManagedFTR(ap, filter='mod_hud', suppress_tt=True)
>>> phi_sm = recon(sx, sy)

(Source code, png, hires.png, pdf)

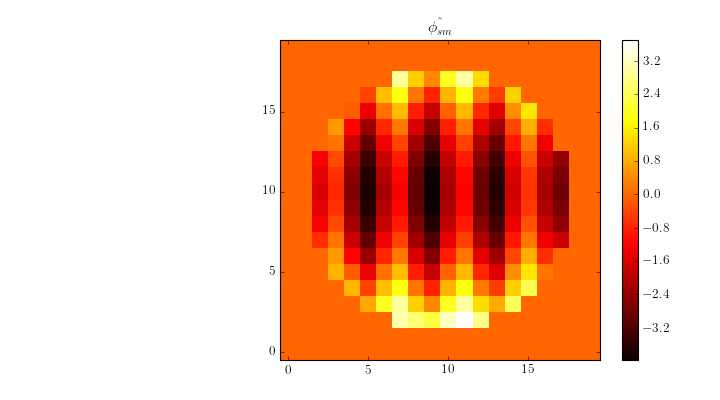
The residuals from this reconstruction are much improved.

(Source code, png, hires.png, pdf)